北海道公立高校入試の理科に出題ミスがあった可能性がある，との記事が2018年3月10日付『北海道新聞』にありました。件の問題は実験結果（といっても机上の計算で作ったもののはずですが）に不備があり，2通りの解答が考えられるというものです。これらについて書いておきたいと思います。理科の大問[５]です。

　（道教委HPより）
この「実験１」に関する問１の(2)はこうなっています：
(2)　物体Aの体積は何 cm³ か，求めなさい。　
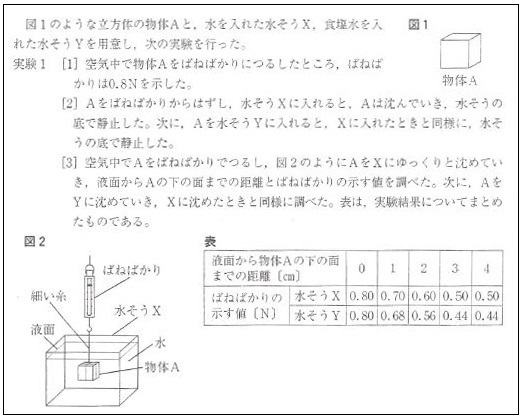
　「表」を見ますと，「液面から物体Ａの下の面までの距離」が 3 cm になったところで「ばねばかりの示す値」が水槽 Ｘ，Ｙ のいずれにおいても一定になっています。これは物体Aにはたらく浮力が一定になったからで，上の「距離」が 3 cm になった時点で物体Aの全体が水中に入ったことを意味します。すなわち，物体Aの高さは 3 cm です。実験の冒頭に「立方体」とありますので，物体Aは 1 辺が 3 cm の立方体ということになります。したがって，求める体積は 3 × 3 × 3 ＝ 27 〔 cm³ 〕 となりそうです（これが公表された正解）。この問題は頻出問題で，多くの受験生はこのように解いたと思います。
ところが，「アルキメデスの原理」によって浮力から計算すると 27 cm³ にはならない，というのが「出題ミスでは」という指摘の中心です。
アルキメデスの原理：
液体の中で静止している物体にはたらく浮力の大きさは，それが押しのけた体積分の液体の重さに等しい
　（本来，液体中でも気体中でも成り立つ原理ですが，ここでは問題に合わせて液体としました）
バネばかりを使って物体Aにはたらく重力（＝重さ）を空気中ではかると 0.80 N ，全部水中に沈めてはかると 0.50 N です。水中では水からの浮力がはたらくのでバネが物体を引く力は空気中よりも小さくていい（楽ができる）わけです。つまり，浮力の大きさは両者の差で 0.80 － 0.50 ＝ 0.30 〔N〕 。 ここでアルキメデスの原理を用いると，物体Aと同体積の水の重さも 0.30 N となります。
さて…
問題文には書かれていませんが， 水の密度は 1 g/cm³ とする…① ことが多い。厳密には温度によって体積が変わり 4 ℃ 付近で最大になるのですが，それは考えない。といいますか，出題者のほうで問題文に「水の密度は 1 g/cm³ とする」と断っておくのが普通です（でないと安心して解答できませんね）。それでも水の密度が 1 g/cm³ であるのは常識といえますし，そう記憶している人が多いでしょう。あとは質量がわかれば体積を求められます。
では質量は？…
これまた問題文には書かれていませんが， 質量 100 g の物体にはたらく重力を １ N とする…② ことが多い。やや厳密には有効数字 2 桁で 0.98 N ですが，本質的に 1 N とみなして構わない場合が多く，中学理科では普通そうします。でも，出題者のほうで問題文に「質量 100 g の物体にはたらく重力を １ N とする」と断っておくのが普通です（でないと…以下同じ）。ということで，物体Aと同体積の水の重さ（＝重力の大きさ）が 0.30 N ですから，その質量は 100 g × 0.30 ＝ 30 g となります。
以上から，
物体Aの体積 ＝ 物体Aが押しのけた水の体積 ＝ 水の質量 ÷ 水の密度
＝ 30 〔 g 〕 ÷ 1 〔 g/cm³ 〕 ＝ 30 〔 cm³〕
となってしまうわけです。
アルキメデスの原理を知っている生徒なら，それを使って「確かめ算」を試みるのは自然なことです。問題文に水の密度や重力の大きさの断りがないので，常識的に上の①，②を仮定して計算したでしょう。すると違う結果が出てしまう。混乱したはずです。この確かめ算を試みるくらいの生徒なら理科は満点近く取れるでしょうから心配は無かったと思いますが，同情を禁じ得ません。
ここで新しい疑問が湧いてしまいます。出題者は自分で解いてみなかったのか？検討者は何を検討したのか？
入試問題を作るくらいだから実力のある教師のはず。大問を設計するにあたり，実験内容に矛盾がないよう注意するのはもちろんですが，自分が立てた問に対する解を自分で考え，別解があれば用意するのが当たり前です。そして，同じ問１の(3)はアルキメデスの原理をモロに使う問ですから，ここでも別解として使ってみるのが自然だと思うのですが。
なお，いまさら代案ではありませんが，物体Aを「立方体」ではなく「直方体」とし，問１(2)では「体積」ではなく「高さ」を問うだけであったら，「 3 cm 」で何ら不都合はなかったでしょう。体積が 30 cm³ なので底面積が 10 cm² となり，矛盾は生じません。
さて，アルキメデスの原理に関しては続きがあります。ここまで長かったので一休みしましょう。よろしければ続きをご覧ください。

では続きです。問１の(3)を見てください。
(3)　水 1 cm³ の質量と食塩水 1 cm³ の質量の比を求め，最も簡単な整数で書きなさい。
アルキメデスの原理を使うのが自然だと思いますので，それで解いてみます。つまり，物体Aにはたらく浮力から物体Aと同体積の水や食塩水の「重さ」を求め，それを質量に換算し，質量を体積で割ればよい。ただし，先にも書いたように質量と重力との換算について断りがありませんし，密度の「比」が必要なだけですから， 密度の比 ＝ 同体積の質量の比 ＝ 同体積の重さの比 と考えます。
物体Ａにはたらｊく浮力は，すべて水中にあるとき 0.80 － 0.50 ＝ 0.30 〔 N 〕 ，すべて食塩水中にあるとき 0.80 － 0.44 ＝ 0.36 〔 N 〕です。アルキメデスの原理により，これらの浮力は物体Aと同じ体積の水や食塩水の「重さ」に等しいので， 密度の比 ＝ 同体積の質量の比 ＝ 同体積の重さの比 ＝ 0.30 N ： 0.36 N ＝ 5 ： 6 となります。
また，先に書いた 質量100gの物体にはたらく重力を１Nとする…② を仮定しますと，物体Aと同体積の水の質量は 30 g ，食塩水の質量は 36 g となるので， 密度の比 ＝ 同体積の質量の比 ＝ 30 g ： 36 g ＝ 5 ： 6 です。
さらに，体積を 30 cm³ として密度を求めれば，水は 30 g ÷ 30 cm³ ＝ 1.0 g/cm³ ，食塩水は 36 g ÷ 30 cm³ ＝ 1.2 g/cm³ となりますので，この比はやはり　1.0 g/cm³ ： 1.2 g/cm³ ＝ 5 ： 6 です。
ところで…
この問がアルキメデスの原理を使わなければ解けないとすると，出題じたいが不適切ということになってしまいます。アルキメデスの原理は中学理科では「発展内容」だからです。
入試は学習指導要領の範囲内，緩めに見ても教科書に書いてある内容から出すべきです。もちろんアルキメデスの原理は重要で，浮力の学習には必修の事項だと思いますが，残念ながら現行の教科書では「発展内容」扱い。「発展内容」だということは，授業で取り上げられない可能性もあるということです。
北海道の公立中学校では，自治体によって東京書籍・教育出版・啓林館の3社のいずれかのものが採用されています。浮力は中１での学習内容で，現行の教科書（2015年に小改訂となった後の）ではアルキメデスの原理は3社とも発展内容。しかも，液体一般としているのは教育出版のみで，東京書籍と啓林館では水だけの話になっている。つまり，食塩水のことは類推するしかありません。しかも，今回の受験生が中１のときに持たされた小改訂前の教科書になりますと，教育出版と啓林館では扱いは同じ（発展内容）ですが，東京書籍では記載がありません。発展内容であれ何であれすべての教科書にそれなりの記載があるのであれば，アルキメデスの原理を知らなければ解けない問題や水を食塩水に置き換えた問題もアリかも知れませんが，教科書によっては記載がないのです。
重要なことは教科書にあろうとなかろうと塾では（たぶん）教えますし，多くの中学でも教えているでしょう。ただし，理科の先生が物理が苦手とか嫌いだったりするとアルキメデスのアの字もない，という可能性だってある。だから教科書はもうちょっとなんとかなっていて欲しいのですが，現状の記載がこうも違うのであれば出題を見合わるべきではなかったでしょうか。
アルキメデスの原理を露わに使わずに解けるか？と考えてみました。
水中の物体にはたらく圧力，つまり水圧は，水面からの深さに比例します。その深さに平面を想定したときにその平面の上にある水の重さによって生じる圧力だからです。だから，水中にある柱状の物体の下面には上面よりも大きな水圧がはたらき，この差が上向きの浮力となります。だから…
浮力は物体の下面と上面にはたらく水圧の差によって生じる。
★水を一般の液体（食塩水とか）に替えても同じことがいえる。
★水でも食塩水でも，浮力がある深さでの圧力を反映しているならば，圧力の原因である液体の重さを反映している。
液体の重さは液体の密度に比例する。
したがって， 浮力の比 ＝ 液体の密度の比 といえるから，
求める比は 0.30 N ： 0.36 N ＝ 5 ： 6
でしょうか。しかしながら。★をつけた部分のようなことの記載は上記3社の教科書には見当たりません。
北海道では，水圧や浮力の問題には「伝統的に」食塩水がよく出るのです。最近では2012年度の大問４，私の知る限り古いところでは2001年の大問４。これらの前例も「発展内容」を出してしまっていたわけですが，前例（実績？）があるからといって繰り返していいことにはならない。出題者は，北海道や全国の入試の過去問の研究はしたのでしょうが，中学生が最も頼りにしているはずの教科書にもよく目を通してほしかったと思います。